Student Research

Ari Geisler '23

Dispersive Shock Waves in Granular Crystals

Supported by the National Science Foundation grant DMS-2107945

Emmanuel Okyere '23

Solitary Waves in a Discrete Conservation Law

Supported by the National Science Foundation grant DMS-2107945

Discrete conservation laws can be used to model phenomena such as traffic flow. Emmanuel studied solitary waves in a discrete conservation law by first deriving a quasi-continuum approximation, and finding exact solitary wave solutions of that model. He compared his analytical approximation against numerical solitary wave solutions of the discrete model.

Bjorn Ludwig '23

Nonlinear Resonance in a Membrane

Supported by the National Science Foundation grant DMS-2107945

Advisor: Chistopher Chong

Bjorn studied nonlinear resonance in a membrane. In Summer 2021, he derived a planar ODE model for the description of the membrane and used fixed-point iterations and perturbation analysis to predict the resonant peaks. In summer 2022, he used COMSOL to conduct finite element simulations of a nonlinear membrane, and to generate parameter values for his ODE prediction, and to compare predictions between the high and low dimensional models.

Sonia Shah '22

Sensitivity Analysis of Basins of Attraction for Nelder-Mead

Advisor: Adam Levy

The Nelder-Mead optimization method is a numerical method used to find the minimum of an objective function in a multidimensional space. Sonia used this method to study functions of two-variables and created images of the basin of attraction of these functions. She used three different methods to create these images named the systematic point method, randomized centroid method, and systemized centroid method, and found that the systemized centroid method appears to be the most precise and effective method at creating the basin of attraction in most cases.

Zach Flood '22 and Juntao Lu '22

Configuration Spaces of Graphs

ZF supported by a National Science Foundation grant DMS-2137628 and JL supported by the Gibbons Fellowship.

Advisor: Eric Ramos

Zach, Juntao, and I spent the summer studying configuration spaces of graphs. More specifically, we studied a particular stochastic winding process that is defined on graph configuration spaces. This process was originally designed to mimic more classical winding processes in the plane, but displays behaviors in this context that are vastly different from its planar analog. It was our intention to produce experimental evidence for a conjecture that postulates that when the winding process is performed on trees, it is refined enough to detect which tree it is being performed on. Juntao and Zach wrote code that ran on Bowdoin’s supercomputing cluster to accomplish this goal. In particular, through their work, we now have evidence for the conjecture far beyond what was originally known, which was for trees of at most 10 vertices.

Gill King '22

Sensitivity Analysis of Basins of Attraction for Gradient-Based Optimization Methods

Advisor: Adam Levy

Gill analyzed the effectiveness of five distinct optimization methods in their ability in producing clear images of the basins of attraction, which is the set of initial pointsthat approach the same minimum for a given function. Effectiveness of the method changes slightly depending on the function, but is generally defined as how closely the basin image models contour information on where the true minima are located, and by the clarity of the resulting image in depicting well-defined regions. Five methods were ranked for their overall effectiveness and consistency across four different objective functions, and sensitivity of the methods to small changes in functions was analyzed.

John Hood '22

The Heavy-Tailed Nature of Noise in Stochastic Gradient Descent

Supported by the Scott and Anne Perper Internship Fund

Advisor: Thomas Pietraho

Stochastic Gradient Descent (SGD) is a surprisingly effective variant of a standard optimization method which underlies modern machine learning techniques. We investigate its stochastic nature, reaffirm that it is heavy-tailed as opposed to normally-distributed, and that this is true irrespective of the underlying data. We also show that the heaviness of the tails for SGD deployed on a neural network increases with the number of parameters in the model.

Madeleine Genereux ’19 and Sean McParland '19

Approximation of Discrete DSWs through PDE approximations

Supported by the NSF through grant DMS-1615037

Advisor: Christopher Chong

Dispersive shock waves (DSWs), which connect states of different amplitude via an expanding wave train, are known to form in nonlinear dispersive media when subject to sharp changes in the initial state. Such extreme changes in a medium can occur when simulating explosions in shock tubes, when gasses or fluids are compressed in a piston chamber, or when water dams break. Sean and Madeline investigated DSWs in a system consisting of masses coupled via nonlinear springs. Using a multiple-scale analysis, they were able to derive PDEs, and from there to approximate the formation and structure of the DSWs. They also conducted numerical simulations to investigate the dynamics.

Kevin Chen '19

Parametric Instability in Granular Chains with Time-Dependent Stiffness

Supported by the NSF through grant DMS-1615037

Advisor: Christopher Chong

A granular chain is a one dimensional network of particles that interact elastically. Kevin studied a granular chain where the stiffness of the particles would vary in time. In particular, the stiffness would vary periodically (according to a step-function). He explored how instabilities can be introduced into the system via variable stiffness through the computation of the dispersion relationship and numerical simulations.

Waverly Harden ’19

Dynamics of Hollow Elliptical Cylinder Arrays

Stipend and travel support by the NSF through grant DMS-1615037; additional travel support provided by the Grua/O’Conell Fund

Advisor: Christopher Chong

Strain-softening materials have gained significant interest in the physics, mathematics and material science communities recently. Most materials that we are familiar with are strain-hardening, meaning as they deform, they become harder to deform. Strain-softening materials have the opposite property; as they deform, they become easier to deform. The dynamics of strain-softening materials in an experimental setting have been rarely studied. For seven weeks, Waverly worked on the modeling and simulation of a system that exhibits strain-softening behavior. It consists of a chain of hollow elliptical cylinders (HEC). She visited the laboratory of her advisors collaborator, Professor Jinkyu Yang, at the University of Washington for the final three weeks of her project to work with the team who developed the concept of the HEC and the experimental set-up. Using the experimental data, she was able to refine her mathematical model. She also worked on an experimental apparatus that controls the impact frequency of the chain, and worked on processing of the experimental data that was acquired through digital image correlation.

Patrick Blackstone ’17

Lp-Harmonic Analysis on SO(3,1)

Supported by Kibbe Institutional Research Fellowship

Advisor: William Barker

The long term goal of this project was to determine the image of the Lp-Schwartz space (0 < p 2) under the operator-valued Fourier transform on the semi-simple Lie group SO(3,1), the proper Lorentz group. This would extend research conducted in the 1980s for the Lie group SL(2,R). Patrick’s work on SO(3,1) mirrored that of Andrew Pryhuber and Justin Dury-Agri for SU(2,1), though SO(3,1) presents a slightly more tractable group since it is only six dimensional as opposed to SU(2,1) which is eight dimensional. Of more significance, SO(3,1) has no “discrete series” of representations, a major simplification over SU(2,1). Patrick concentrated on the more algebraic foundations of the project, working out the necessary algebraic structure theory of SO(3,1). As a sophomore Patrick did not have the background to explore the more analytic aspects of the representation theory of SO(3,1), a requirement for tackling the ultimate Lp-Schwartz space problem.

Parikshit Sharma '17

Neural networks and transfer learning models in image subject classification

Advisor: Thomas Pietraho

In transfer learning, machine learning models trained to perform a specific task are retrained and repurposed to perform complementary tasks. Often, lower order features learned by a neural network in one context can be reassembled into higher-order features that are useful in another. In this project, we set out to classify the subject area of a book based solely on the image of its cover. Using transfer learning from a number of pretrained image classification neural nets such a Google's Inception, the classification accuracy of our new models exceeded 70 percent. This is near the accuracy of a human asked to perform the same task.

Sophie Bèrubè '16 and Tara Palnitkar '16

Diestel-Leader Groups are Graph Automatic

Supported by the NSF through grant DMS-1105407

Advisor: Jennifer Taback

Automatic groups were introduced in the 1990's in order to classify the groups associated with three dimensional "shapes," or manifolds. A group is a set with an operation which satisfies certain basic properties, such as the integers under addition, and in general captures the symmetry of some, perhaps complicated, object. In an automatic group, simple computational machines called finite state automata are used to describe the group elements as well as the group multiplication. These automata streamlined computation within the group, leading to expedited solutions of geometric and computational questions in group theory. Unfortunately, not all three manifold groups fell into this category, and so the definition was extended to that of graph automatic groups. The latter retained many of the computational advantages of automatic groups while enlarging the class considerably.

Sophie and Tara worked to show that a new infinite family of groups, called Diestel-Leader groups, or higher rank lampligher groups, are graph automatic. This required gaining a deep geometric and algebraic understanding of these groups, as well as learning about different types of finite state automata. Along the way, they proved that some related infinitely generated groups were also graph automatic. This work will appear as an article in the Journal of Algebra.

Jacob Hart ’17 and Carina Spiro ’18

Nonlinear Energy Harvesting

Stipends supported by the Maine Space Grant Consortium, travel supported by the NSF through grant DMS-1615037

Advisor: Christopher Chong

The last several decades as seen a burst of research activity in vibration energy harvesting, which deals with the conversion of mechanical energy (such as vibration) into electrical energy. Most commercial energy harvesters are based on linear responses, which have a relatively restricted range of vibration frequencies where energy harvesting is efficient. Jake and Carina explored the integration of novel aspects of nonlinear wave equations to try to harvest energy in new ways. In particular,they studied an array of cantilevered beams that are coupled via magnetic links. For the first six weeks of the project, they worked on the modeling of the system, its numerical simulation, and the computation of periodic orbits. They visited the laboratory of their advisors collaborator, Professor Chiara Daraio, at the ETH Zurich for their final two weeks to work with the team developing the experimental set-up of the array of cantilevers. Using the experimental data, they were able to refine their mathematical model.

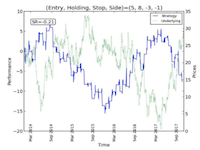
Daniel Byrnes '15

Extreme Value Theory and Backtest Overfitting in Finance

Advisor: Thomas Pietraho

Using tools from extreme value theory, Daniel proposed a new statistic, the minimum back test length at level p, to determine whether a multi-parameter investment strategy has the potential to be overfit and its future returns may be poorly predicted by its performance on historical market backtest data.

Maxwell Wolf '15

Independent Summer Study: Exploring Chaos Theory Through Art

Advisor: Michael King

Max studied Chaos Theory, with the goal to tie together both his major in mathematics and his minor in visual arts. Chaos modeling describes non-linear dynamic systems like weather systems and turbulence in liquids and gasses, and creates incredibly intricate images of fractals. Max's studies culminated in a campus-wide exhibit at the Main Gallery in the Edwards Center for Art and Dance where he demonstrated the beauty of chaos while simultaneously defining, explaining, and attempting to teach the mathematical complexity of the theory to the gallery viewers. Max says this project allowed him to explore and appreciate how math and art intersect and illuminate each other.

Andrew Pryhuber ’15 (Kibbe Institutional Research Fellowship)

Summer Research 2014 and Honors Project: The Structure and Unitary Representations of SU(2,1)

Advisor: William Barker

The long term goal of this project was to determine the image of the Lp-Schwartz space (0 < p 2) under the operator-valued Fourier transform on the semi-simple Lie group SU(2,1). This would extend research conducted in the 1980s for the Lie group SL(2,R). However, the dimension of SL(2,R) is three while the dimension of SU(2,1) is eight, making the analysis of SU(2,1) both more difficult and more interesting than SL(2,R). Andrew worked in a partnership with Justin Dury-Agri during the summer of 2014 and into that fall. Together they worked out the needed structural apparatus for SU(2,1) (e.g., the root space decomposition). They also mastered some intricate infinite dimensional representation theory, in particular the basics of the “principal series representations” and the “discrete series representations” for SU(2,1). These are of critical importance for even describing the operator-valued Fourier transform on the Lp-Schwartz space of SU(2,1) and its conjectured image space. To fully determine this image requires proving that the transform map is a continuous bijection with a continuous inverse, not a trivial undertaking. Andrew continued to pursue various parts of this program as an Honors project until time ran out. His Honors thesis describes the results of his project.

Justin Dury-Agri ’15 (Surdna Foundation Research Fellowship)

Summer Research 2014 and Independent Study: Lp-Harmonic Analysis on SU(2,1)

Advisor: William Barker

The long term goal of this project was to determine the image of the Lp-Schwartz space (0 < p 2) under the operator-valued Fourier transform on the semi-simple Lie group SU(2,1). This would extend research conducted in the 1980s for the Lie group SL(2,R). However, the dimension of SL(2,R) is three while the dimension of SU(2,1) is eight, making the analysis of SU(2,1) both more difficult and more interesting than SL(2,R). Justin worked in a partnership with Andrew Pryhuber during the summer of 2014 and into that fall. Together they worked out the needed structural apparatus for SU(2,1) (e.g., the root space decomposition). They also mastered some intricate infinite dimensional representation theory, in particular the basics of the “principal series representations” and the “discrete series representations” for SU(2,1). These are of critical importance for even describing the operator-valued Fourier transform on the Lp-Schwartz space of SU(2,1) and its conjectured image space.

Lauren Skerritt '14

Mathematical Modeling of the American Lobster Cardiac Muscle Cell: An Investigation of Calcium Ion Permeability and Force of Contractions
Advisor: Adam B. Levy (with Amy Johnson and Olaf Ellers)
Lauren developed a mathematical diffusion model of the myofibril (muscle cell) to simulate calcium cycling in the lobster cardiac muscle cell. The amplitude and duration of the force curves produced by the model empirically mirrored that of the experimental data over a range of calcium diffusion coefficients (1-16), nerve stimulation durations (1/6-1/3 of a contraction period), and frequencies (40-80 Hz). The characteristics that alter the response of the lobster cardiac muscle system are stimulation duration (i.e., burst duration), burst frequency, and the rate of calcium diffusion into the cell’s cytoplasm. For this reason, she developed protocols that allow parameters representing these characteristics in the calcium-force model to be determined from isolated whole muscle experiments on lobster hearts (Phillips et al., 2004). These parameters are used to predict variability in lobster heart muscle function consistent with data recorded in experiments.

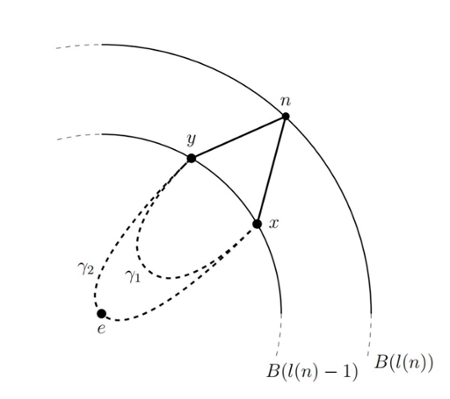Peter Davids '14

Convexity properties of the Diestel-Leader groups Τ₃(2)
(Supported by the NSF through grant DMS-1105407)

Advisor: Jennifer Taback

A mathematical group is a set with an operation satisfying certain basic properties; for example, the integers under addition form a group, as do the real numbers under addition. A Cayley graph is a geometric model of a group -- that is, we hope to view any group much as we think of the real numbers as comprising the number line. This allows us to envision the geometry of a group. We can ask questions about whether spheres in this group geometry are "round" and whether they get larger the way they do in Euclidean space as the radius increases. Almost convexity is a geometric property which tries to answer these questions about the "roundness" of spheres in the geometry associated to a group. In a group which is not almost convex, spheres of larger and larger radii have missing "fingers," quite contrary to our notions of spheres of increasing radii from high school geometry.

In this project, Peter investigated convexity properties for the Diestel-Leader groups, first understanding their geometric model, and then focusing on one example from this family, denoted $\Gamma_3(2)$. The notation means that the geometric model of the group is contained in the product of three regular trees of valence 3. Peter showed that this group is not almost convex, but that it satisfies a weaker convexity condition known as minimal almost convexity.

Sharif Younes '13

NSF-funded Research student: Finite state machines and Thompson’s group F

Advisor: Jennifer Taback

Finite state machines such as finite state automata and pushdown automata are used in computer science to model simple “languages.” In group theory, one often hopes to show that the elements of a group can be described by one of these machines and that such a machine can recognize group multiplication; if so, many computational questions are easily solvable in the group. Such groups are called “automatic” or “context-free” depending on the type of machine used. Sharif is investigating whether Thompson’s group F is “Cayley graph context-free” by constructing pushdown automata recognizing group elements and multiplication. This project lies at the intersection of mathematics and theoretical computer science.

headshots of Emma Cutler and Amanda Gartside

Emma Cutler '13, Amanda Gartside '12, and Carolyn Mayer '13

Clare Boothe Luce Fellow, NSF Math Climate Research Network grant

Advisor: Mary Lou Zeeman

This team works with the Mathematics and Climate Research Network (MCRN) to study dynamical models of paleoclimate. The research goal is to use tools of differential equations and dynamical systems to investigate the feedback effects of different climate processes on each other and on global climate. We are focusing on the interaction between carbon, earth orbitals and ice-albedo feedback in the earth’s glaciation cycles.

Felicity Hills '13, Jane Carpenter '13, Elena Crosley '13

Computational Sustainability NSF grant

This team works on the fishery models. The goal is to develop a model that can include the ecological interactions of some key species. This requires adding some age structure to the classic models.

Sharon Ulery '11

Independent Study: Properties of sets of elements in Thompson’s group F

Advisor: Jennifer Taback
This project involved learning about Thompson’s group F, an example of an infinite, finitely generated group. Sharon used the techniques developed by Susanna Kimport as part of her honors project to select large sets of elements of this group, and statistically analyze certain properties of these elements. These sets were not taken randomly, and were used to verify that Kimport’s algorithms ran equally quickly on a variety of types of elements.

Brian Wu '11

Honors Thesis: Algebraic Geometry
Advised by Thomas Pietraho

Emma Chiappetta '11

Cayley-Klein Geometries.
Advisor: William Barker
Emma studied the Cayley-Klein geometries from several different viewpoints, most notably those of Jürgen Richter-Gebert and I. M. Yaglom. She read in detail original papers by Klein, Beltrami, and Sommerville, and proved several of her own conjectures about these geometries. She concentrated on the classification of the planar Cayley-Klein geometries as nine subgeometries of the projective plane—subgeometries that include Euclidean hyperbolic, elliptic, Minkowskian, and Galilean. This supports Cayley's famous quote that "Projective geometry is all geometry."

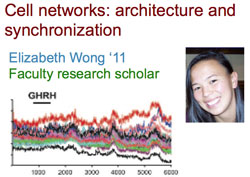Elizabeth Wong '11

Advisor: Mary Lou Zeeman
Elizabeth modeled networks of cells in the pituitary. Recent experiments in rodents show that each cell type in the pituitary forms a 3-d network of chains, connected by cell clusters. As the animal grows, the cluster-to-chain ratio in the cell network changes. This change in network architecture correlates with a more synchronized release of hormone from the cells. Elizabeth used computational models to investigate whether the change in network architecture can explain the increased synchrony in hormone output.

Christina Argueta '11

Honors Project: Constructing minimal length representatives for elements of Thompson’s group F
Advisor: Jennifer Taback
When studying a finitely generated infinite group described using generators and relations, a natural question is to ask for the minimal number of generators necessary to represent a given group element. Christina studied this problem for Thompson’s group F, building on work of Professor Taback and Micah Miller ’04. Christina was able to give combinatorial conditions governing the creation of these ``minimal length representatives” for many elements of this group. Her results were based on a combination of group theory and insight into the particular group studied, and illustrated the interaction between the varied techniques used to study this group.

Harrison Chapman '11

Honors Thesis: Nilpotent Orbits of Lie Groups
Advised by Thomas Pietraho

Will Richard '11

Independent Study: Folner sets and amenability in Thompson’s group F
Advisor: Jennifer Taback
This project involved studying one of the most famous open questions related to Thompson’s group F, and investigating whether one could produce sets of elements with certain graph-theoretic properties within the Cayley graph of this group. This first involved an understanding of what a Cayley graph of a group is, and how one associates a geometric picture with a particular group. To complete this project, Will studied a variety of techniques developed by research mathematicians to understand the elements of this group and multiplication within the group. These techniques included algebraic, geometric and combinatorial aspects. Some of Will’s numerical estimates relied on counting formulae from combinatorics related to counting binary trees with particular properties. Will also used simulations constructed with the computer program Mathematica as part of his project.

Kim Ayers '10

Stochastic Perturbations of the Fitzhigh-Nagumo Equations
Advisors: Adam Levy and Mary Lou Zeeman
Kim used stochastic perturbation techniques she learned in a summer research project at Iowa State U. to model the effect of neural noise in the context of the classical Fitzhugh-Nagumo equations for the nerve impulse. The classical equations can capture action potentials and tonic firing of a neuron, but not the more complex patterns of bursting (periods of firing interleaved with periods of quiescence). Kim incorporated stochastic noise into the Fitzhugh-Nagumo equations, representing stochastic opening and closing of ion channels, for example, and showed that the stochastic model was able to exhibit a range of bursting behaviors observed in neurons.

Mark McGranaghan '09

Independent Study) Random selection of elements in Thompson’s group F
Advisor: Jennifer Taback
This project involved formalizing the notion of selecting an element of a group at random. The group used was Thompson’s group F, and a technique to select elements uniformly published in a paper by Elder, Fusy and Reichnitzer was implemented. Mark then used his program to select large sets of random elements and gather statistical data about their “geometric” properties. Every element of Thompson’s group can be represented by a pair of finite rooted binary trees, and some unexpected conclusions were found in statistics about the shape of these trees.

Susanna Kimport '09

Honors Project: An algorithm for computing word length in Thompson’s group F
Advisor: Jennifer Taback
This project investigated the feasibility of implementing a computational technique developed by Matt Horak, Melanie Stein and Jennifer Taback for computing word length of elements in Thompson’s group F. After showing that implementing the simplest case of the technique is an NP-complete problem, Kimport developed a practical “smart brute-force” algorithm which computed the correct values very quickly. This project involved a mix of techniques from advanced mathematics, theoretical computer science, and computer

Anh Tran '10

Neural Nets and Finance
Advised by Thomas Pietraho

Erin Taylor '09

Feedback in Lobster Cardiac Oscillations
Advisors: Patsy Dickinson, Adam Levy and Mary Lou Zeeman

Liz Chertavian '09

Inversion of a Firn Air Diffusion Model to Determine Atmospheric Gas Concentration Histories
Advisors: Mark Battle, Adam Levy and Mary Lou Zeeman
As snow falls onto a glacier, it compacts the snow below it slowly until it becomes ice. This glacial snow on top of the ice is called firn. While ice has bubbles of air surrounded entirely by ice, the firn has channels of open air space, called the firn air, that run from the surface of the snow down to the close off region where the snow becomes denser ice. The goal of Liz’s thesis was to improve the mathematical method for determining the atmospheric history of concentrations of greenhouse gases from their current concentrations in the firn air channels. This firn air contains the history for the last 100 years (then the ice cores take over).

Ben Johnson, Network Similarity and Shape Recognition, Fall, 2011.
Advised by Thomas Pietraho

Octavian Neamtu, Generalization of the Landmark Method in Shape Recognition, Fall, 2011.
Advised by Thomas Pietraho

Arsenyi Sheydvasser (Honors Thesis), Advanced Functional Analysis, Fall, 2011.
Advised by Thomas Pietraho

Jonathan Ackerman, Generating Functions and Phylogenetic Trees, Spring, 2011.
Advised by Thomas Pietraho

Sean Wilner (Honors Thesis), Algebraic Geometry, 2010–2011.
Advised by Thomas Pietraho

Leah Wolberg (joint with N. Kieserman), Orbifolds, Spring, 2010.
Advised by Thomas Pietraho

Sean Wilner (joint with N. Kieserman), Orbifolds, Spring, 2010.
Advised by Thomas Pietraho

Mark McGranaghan, Neural Nets and Pattern Recognition, Fall, 2009.
Advised by Thomas Pietraho

Michael Krohn, Financial Mathematics, Spring, 2009.
Advised by Thomas Pietraho

Sarah Landrum, Financial Mathematics, Spring, 2009.
Advised by Thomas Pietraho

Mathematics

Student Research

Ari Geisler '23

Emmanuel Okyere '23

Bjorn Ludwig '23

Sonia Shah '22

Zach Flood '22 and Juntao Lu '22

Gill King '22

John Hood '22

Madeleine Genereux ’19 and Sean McParland '19

Kevin Chen '19

Waverly Harden ’19

Patrick Blackstone ’17

Parikshit Sharma '17

Sophie Bèrubè '16 and Tara Palnitkar '16

Jacob Hart ’17 and Carina Spiro ’18

Past Student Research

Daniel Byrnes '15

Maxwell Wolf '15

Andrew Pryhuber ’15 (Kibbe Institutional Research Fellowship)

Justin Dury-Agri ’15 (Surdna Foundation Research Fellowship)

Lauren Skerritt '14

Peter Davids '14

Sharif Younes '13

Emma Cutler '13, Amanda Gartside '12, and Carolyn Mayer '13

Felicity Hills '13, Jane Carpenter '13, Elena Crosley '13

Sharon Ulery '11

Brian Wu '11

Emma Chiappetta '11

Elizabeth Wong '11

Christina Argueta '11

Harrison Chapman '11

Will Richard '11

Kim Ayers '10

Mark McGranaghan '09

Susanna Kimport '09

Anh Tran '10

Erin Taylor '09

Liz Chertavian '09