Geometry in Our Modern World
By Tom PorterGeometry may be one of the oldest branches of mathematics, but it’s much more than a theoretical subject. It’s part of our everyday lives, says Professor Jennifer Taback, and key to understanding many aspects of our modern world.

Architecture, mapmaking, video games, data representation, and electoral politics are some of the real-world applications of geometry studied by students in two classes taught by Taback in the fall 2020 semester. Both classes extend the ideas of Euclidean geometry taught in a standard high school to include the basics of spherical and hyperbolic geometry. In both, she emphasized modern applications of both Euclidean and non-Euclidean geometry.
- In Math 2404, students use modern approaches to geometry in order to study gerrymandering and to analyze how maps are made.
- In Math 3404: Advanced Topics in Geometry, they worked on deeper versions of the same projects, as well as some additional topics like using geometry for data visualization and understanding Escher’s artwork from a mathematical perspective. For example, the Escher (see image) is a tessellating (repeating) pattern in the hyperbolic plane.

Applications of mathematics, specifically geometry, to electoral redistricting and the challenge of combatting gerrymandering is a current topic of study among many mathematicians, pioneered by Professor Moon Duchin of Tufts University. Multiple gerrymandering cases have been heard in recent years by the Supreme Court, and shaping district boundaries has social, political, and economic impacts on society.
Mathematically, gerrymandering touches on an old mathematical problem called the isoperimetric problem, which relates the perimeter of a region to its area. Students studied this problem, as well as different ways one can mathematically assess gerrymandering. They took a hands-on approach to gerrymandering and explored software that allowed them to attempt to equalize representation among existing districts in their state.
To highlight several modern applications of geometry, Taback arranged a series of special lectures given by experts from MIT, Colby, and other institutions.
The first, by YouTuber CodeParade, was on implementing a hyperbolic world in a video game context.
The second, by MIT professor Octavian Ganea, described cutting-edge work in machine learning using hyperbolic geometry to obtain embeddings of hierarchical data sets.
The third, by Colby College professor Scott Taylor, discussed how hyperbolic geometry can be used to model large data sets, such as the router connections underlying the world wide web.
Finally, curator Kevin Adkisson from the Cranbrook Center for Collections and Research gave an inspiring talk on geometry in architecture. This lecture was delivered from a Frank Lloyd Wright house, and Adkisson was able to tour the house over Zoom, highlighting Wright’s innovative use of geometry in real time.
Some of Taback’s students from Math 2404 shared their impressions of the course:

“Geometry has completely changed how I view the world around me and has led me to reexamine all the geometric facts and theorems I had just assumed to be true in high school,” said Sarah Clarke ’23. This semester, Clarke and her classmates looked at three different types of geometry—Euclidean, spherical, and hyperbolic geometry—which each have a different set of guiding principles.
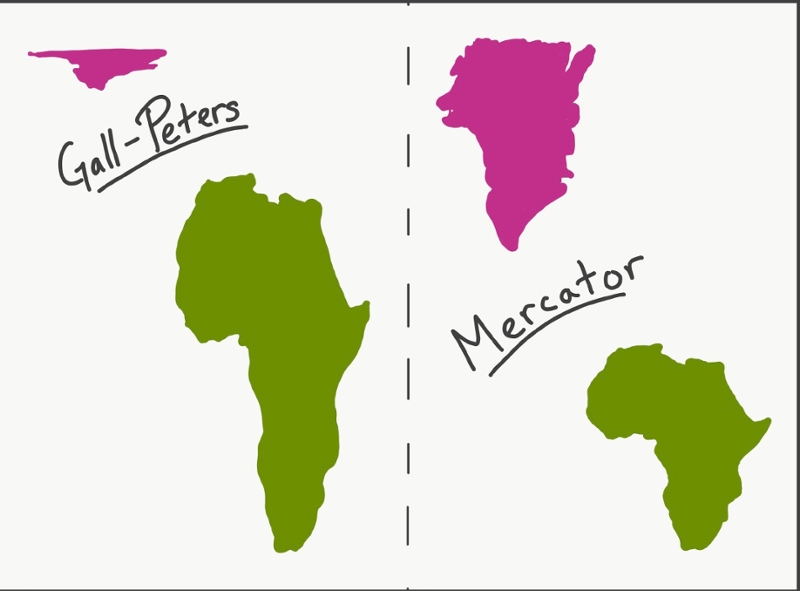
For her map project, Clarke chose to study the Hobo-Dyer projection after learning that it better preserves the true proportions of the areas represented. “Growing up, all of my textbooks used the Mercator projection, which largely skews the size of certain countries,” she said.
“For example, it makes Greenland look the size of Africa, while Africa is actually fourteen times larger! I learned that the Hobo-Dyer map is more equitable for a variety of reasons: In addition to preserving the proportional sizes of countries, it also shows the world in a different perspective than we're used to, as on one side it has a map with the South Pole at the top. This change in perspective urges people to challenge what they always had considered to be the ‘right’ way to view the world.”

Benjamin Mason ’22 said his favorite aspect of the course was Taback's focus on teaching the ways in which geometry shows up in everyday life, something that was enhanced by the host of guest lecturers.
“Professor Taback has made the content feel relevant,” he added, “which can be an uphill battle with upper-level math courses!”

Mason’s project was called Map Projections: The Art of Imperfection. “Our map projects focused on spherical geometry and the issue of trying to project the Earth (which is technically an oblate spheroid) onto a 2D map,” he explained.
“There is no way to make this projection without distorting certain components of reality, whether that be the distance, size, or shape of objects on the map. Thus, mapmakers are forced to make decisions over which elements of the map to prioritize."
For his project, Jonas Eichenlaub ’22 gave an overview of the Gall-Peters map projection, which, he explained, preserves the area of countries at the expense of their shape, so everything looks stretched vertically.
“The Gall-Peters projection rose to prominence in the twentieth century because it more accurately displays the size of areas around the equator than the Mercator projection, meaning that Africa looks as big as it truly is. Portraying Africa as its true size was seen as a way to ‘decolonize’ our perception of the world,” said Eichenlaub, “but what surprised me as I worked on my project was that, while well intentioned, the Gall-Peters projection is actually a pretty poor projection mathematically. Geometry taught me how to assess the usefulness of the Gall-Peters projection not just based off the social justice reasons to use it, but also the geometric reasons not to.”

Eichenlaub said he found the class unexpectedly eye-opening. “It showed me a world of geometry beyond the area formulas and triangle congruence theorems that everyone learns in high school geometry.” He said he had to be convinced to take this class because he thought it would be too theoretical and boring. “But throughout this course I've come to understand that geometry covers topics I encounter on a daily basis, like video games, GPS, and so on.”
Eichenlaub also said geometry takes the things he always assumed to be true and turns them on their head. “For example, changing one tiny assumption about the basis of Euclidean geometry completely changes how geometry works, forcing me to question which geometric truths I can take as given from the physical world and which I need to justify.”
More map facts: useful links from Professor Taback:
- To explore map projections, start with this video, which explains why creating an accurate map is mathematically impossible.
- To understand how the Mercator projection distorts the area of countries, explore this app, which allows you to compare the size of a country on a standard map with its actual size.
- To explore further, this website lists a variety of map projections that create alternate maps, each with a different goal.
Math YouTuber CodeParade explains Non-Euclidian geometry:



